Vor 42 Jahren entdeckten Jocelyn Bell und Antony Hewish den ersten Pulsar und bestätigten damit die Existenz von Neutronensternen. Doch was sind Pulsare überhaupt?
Autor: Christine Gnahm

(Bild: Roberto Saglia)
Geschichtliches
Die „Geschichte“ der Neutronensterne beginnt 1932 mit der Entdeckung des Neutrons durch James Chadwick. Noch im gleichen Jahr diskutiert Lew Landau die Möglichkeit, dass stabile Sterne aus Neutronen existieren könnten. Diese Idee wird zwei Jahre später von Walter Baade und Fritz Zwicky aufgegriffen, die bei der theoretischen Beschreibung von Supernova-Explosionen den Neutronenstern als mögliches Endprodukt annehmen. 1939 rechnen J. R. Oppenheimer und G. M. Volkoff erste Modelle für Sterne aus entarteter Neutronenmaterie. In dieser Zeit wird vermutet, dass Neutronenkerne die Energiequelle massiver normaler Sterne sein könnten. Doch mit dem Verständnis der thermonuklearen Fusion flaut das Interesse an Neutronensternen wieder ab – nicht zuletzt, da es kaum möglich erscheint, solche kompakten und leuchtschwachen Objekte zu beobachten. Erst knapp dreißig Jahre später rücken die Neutronensterne wieder in den Mittelpunkt des Interesses: 1967 entdecken Jocelyn Bell und Antony Hewish den ersten Pulsar.
Pulsare
Pulsare zeichnen sich dadurch aus, dass sie elektromagnetische Strahlungspulse in sehr regelmäßigen Abständen aussenden. Bei den meisten Pulsaren liegt die beobachtete Strahlung im Radiobereich, es gibt allerdings auch Pulsare, von denen optische, Röntgen- und sogar Gamma-Strahlung beobachtet werden kann. Die Perioden der Pulse liegen zwischen 1,5 ms und 11 s und sind außergewöhnlich stabil – so stabil, dass manche Pulsare als Uhren verwendet werden können, deren Präzision Atomuhren Konkurrenz macht. Jedoch bleibt die Periode nicht auf Dauer konstant, sondern wird mit der Zeit länger. All diese Eigenschaften lassen nur eine Erklärung zu, die 1968 von Gold vorgeschlagen wurde: Bei den Pulsaren handelt es sich um schnell rotierende Neutronensterne mit extrem starken Magnetfeldern bis hin zu 1015 Gauss (zum Vergleich: Das Erdmagnetfeld ist etwa 0,5 G stark). Sowohl die hohen Frequenzen als auch die starken Magnetfelder rühren von der Entstehung der Neutronensterne in Supernova-Explosionen her, bei denen der verbleibende Teil des ursprünglichen Sterns auf einen Radius von etwa 12 km zusammenschrumpft. Da gleichzeitig sein Drehimpuls erhalten bleibt, beschleunigt sich die Rotation und das ursprünglich schwache Magnetfeld wird extrem verstärkt.
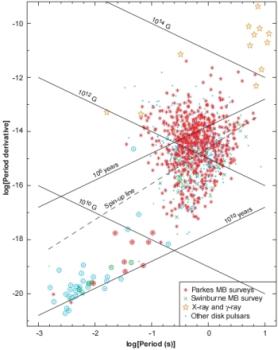
(Bild: R. N. Manchester, „Observational Properies of Pulsars“, Science 304, 542-547 (2004))
Wie ein Dynamo erzeugt der schnell rotierende Neutronenstern mit seinem starken Magnetfeld elektrische Feldstärken um
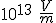
an seiner Oberfläche, mit denen Teilchen zu ultrarelativistischen Geschwindigkeiten
beschleunigt werden. Dadurch kommt es zu einer lawinenartigen Elektron-Positron-Paarerzeugung und schließlich zur gerichteten Abstrahlung elektromagnetischer Wellen.
Der genaue Prozess dieser Abstrahlung ist noch nicht verstanden. Viele beobachtete Eigenschaften können jedoch mit einem einfachen Modell erklärt werden, in dem man sich den Neutronenstern als magnetischen Dipol vorstellt. Dabei wird die Strahlung entlang der magnetischen Feldlinien abgegeben, die von den magnetischen Polen ausgehen. Die Achse des magnetischen Dipols fällt in der Regel nicht mit der Rotationsachse des Sternes zusammen und der Kegel, in dem die Abstrahlung der elektromagnetischen Wellen stattfindet, rotiert zusammen mit den magnetischen Polen. Dabei entsteht ein Leuchtturmeffekt: Nur, wenn der Kegel die Erde streift, können wir ein Signal beobachten. Deswegen sehen wir Pulse mit der Rotationsfrequenz des Neutronensterns. Die für diese Abstrahlung benötigte Energie wird bei gewöhnlichen Pulsaren der Rotationsenergie entzogen. Dadurch wird die Rotationsperiode mit der Zeit länger. Diese Periodenzunahme
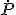
liegt typischerweise bei etwa 10-15. Interessanterweise kann die Verlangsamung der Rotation dazu genutzt werden, das Alter des Pulsars t abzuschätzen. Dazu setzt man im Dipolmodell die Abnahme der Rotationsenergie mit der abgestrahlten Energie eines magnetischen Dipols gleich. Definiert man sich als spezifische Größe die charakteristische Zeit
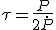
, so kann man einen direkten Zusammenhang zwischen
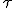
und dem Alter t des Neutronensterns berechnen:

für f0 << fi.
Dabei ist f0 die heute beobachtete Rotationsfrequenz und fi die Rotationsfrequenz zum Zeitpunkt t=0. Geht man von der – unrealistischen – Annahme aus, dass der Pulsar direkt nach seiner Entstehung unendlich schnell rotiert ist, kann der zweite Term vernachlässigt werden. Da die anfängliche Rotation des Pulsars auf jeden Fall langsamer war, stellt
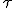
eine obere Grenze des wahren Sternalters dar. Pulsare mit einer Periode von etwa 1 s und einer Periodenänderung von ungefähr 10-15 sind demnach ein bis zehn Millionen Jahre alt.
Die erste Beobachtung, die die Erklärung von Pulsaren als rotierende Neutronensterne bestätigt, erfolgt 1968. In diesem Jahr wird ein Pulsar im Krebsnebel entdeckt. Der Krebsnebel entstand bei einer Supernova in der Milchstraße, die im Jahr 1054 von chinesischen, japanischen und arabischen Astronomen beobachtet wurde. Sie war so hell, dass man sie sogar bei Tag sehen konnte. Bei seiner Explosion schleuderte der sterbende Stern seine äußere Hülle ins Weltall, die mit großer Geschwindigkeit auf das interstellare Medium prallte und dadurch als leuchtender Nebel sichtbar war. Im Zentrum des Krebsnebels blieb als letzter Überrest des Sternes ein Pulsar. Er rotiert sehr schnell in nur 30 ms. Aus der Abbremsung seiner Rotation kann man als charakteristisches Alter
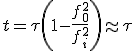
=1.240 Jahre bestimmen – was gut mit dem tatsächlichen Alter von 954 Jahren übereinstimmt.
Eine weitere Bestätigung von Golds Theorie ist die Beobachtung, dass der aus der Abbremsung berechnete Energieverlust in etwa dem Betrag entspricht, der zum Antreiben des Krebsnebels notwendig ist. Der Krebspulsar kann damit als erster Pulsar mit einem Supernova-Überrest in Verbindung gebracht werden.
Millisekundenpulsare und Magnetare
In Abbildung 2 sind neben den gewöhnlichen Radiopulsaren, die eine Periode um 1 s besitzen und den Großteil der beobachteten Pulsare ausmachen, noch zwei weitere Gruppe von Pulsaren zu sehen. Links unten im Diagramm, mit sehr viel kürzeren Perioden (im Millisekundenbereich), schwächeren Magnetfeldern (108-109 G) und einer vier bis sechs Größenordnungen langsameren Abbremsung, liegen die Millisekundenpulsare (MSPs). Sie sind ein bis zehn Milliarden Jahre alt und damit sehr viel älter als normale Pulsare. Die meisten Millisekundenpulsare befinden sich in Doppelsternsystemen. Man vermutet, dass sie ursprünglich alte, langsam rotierende Pulsare waren. Durch Akkretion – die Übertragung von Masse und Drehimpuls – von ihrem Begleitstern werden sie in einer Art „Recycling-Prozess“ zu neuer und schneller Rotation angetrieben.

(Bilder: NASA)
Eine andere Pulsarfamilie sind die Magnetare. Sie befinden sich rechts oben im Diagramm und sind nur bei hohen Energien im Röntgen- oder Gamma-Bereich detektierbar. Sie besitzen die größten Magnetfelder um 1015 G. Man geht davon aus, dass bei ihnen – im Gegensatz zu Radiopulsaren und MSPs – die Abstrahlung nicht durch die Rotationsenergie, sondern hauptsächlich durch den Zerfall der extrem starken Magnetfelder angetrieben wird.
Mehr über Neutronensterne können Sie im nächsten Teil dieser Artikelreihe nachlesen, der in Kürze erscheint.
